
SPIは多くの企業が取り入れている適性検査の一つですが、非言語分野の定番問題「推論」に悩まされる学生は少なくありません。
そこで本記事では、推論が難しいと感じている学生のために、解き方のコツや具体的な対策方法を紹介します。また、記事の後半では推論の問題例も掲載しているので、ぜひ実際に解いてみてください。
SPIの推論とは?
SPIの推論は、数的な能力を問う「非言語分野」で頻出の問題です。回答するためには、与えられた情報を整理して事実を把握し、正しい結論を推測する必要があります。
ただ、推論の答えを導き出すために、難しい計算式や前提知識は必要ありません。論理的思考力と基礎的な計算能力が問われる問題なので、解き方のコツをマスターすれば選択肢の中から正解を選ぶことができるでしょう。
SPI推論の対策は必要?
SPIの問題は基本的に中学・高校レベルですが、推論はとくに難易度が高いため事前に対策をしておく必要があります。また、非言語分野では四則演算や順列、組み合わせなどの問題が出されますが、推論も頻出問題の一つです。
SPIを通過するには幅広い問題に答える必要があるため、苦手だからといって対策しないままでは次の選考に進めないかもしれません。これからSPI対策を進める方は、推論を含め苦手な分野の克服に努めましょう。
SPI推論問題を解くコツ
ここからは、推論問題を解く際のコツを3つ紹介します。
【SPI推論を解くコツ1】文章を丁寧に読む
推論の問題を解くときは、問題文を丁寧に読むことが重要です。SPIは制限時間が設けられているために焦ってしまう人もいますが、読み間違えて不正解の選択肢を選んでしまうことも珍しくありません。
推論は他の問題よりも制限時間が長く設定されているため、落ち着いて文章を読み情報を整理しましょう。
【SPI推論を解くコツ2】紙に書き出す
推論の問題を頭の中で考えていこうとすると、途中で混乱してしまう可能性もあります。そこでおすすめなのが、メモを紙に書き出していくことです。考えられるパターンや条件を表・図・グラフなどに書き出すことで、情報を視覚的に整理できます。
頭の中で考えよりも思考の抜け漏れを防ぎやすいため、就活生が失敗しがちなケアレスミスも減らせるでしょう。
【SPI推論を解くコツ3】問題のパターンに慣れる
例年、SPIの問題は出題内容がパターン化されており、推論の問題も例外ではありません。推論の問題例は記事の後半で紹介していますが、頻出のパターンは以下の7つです。
順序
整数
割合
平均
位置
対戦(リーグ戦・トーナメント戦)
初めて推論の問題を見ると戸惑うかもしれませんが、時間をかけて解き方を身につけることで、焦らず正解を導き出すことができます。問題集を使って解き慣れておけば、SPI本番でもスムーズに回答できるようになるでしょう。
SPIの対策方法
推論をはじめ、SPIの対策をおこなうときは問題を繰り返し解くだけでなく、スキマ時間を活用したり、本番と同じ環境で受けたりするのがおすすめです。
SPIを通過して次の選考に進むためにも、それぞれの対策方法をチェックしておきましょう。
【SPI推論の対策方法1】繰り返し解く
推論を対策するのであれば、問題集を最低3周以上は解きましょう。1冊の問題集を3周以上解けば、問題のパターンを掴めるほか、自分が間違えやすいポイントに気づくことができます。
初めのうちは時間を気にせず問題をじっくりと考え、問題形式を理解して回答パターンを覚えるのもおすすめです。
【SPI推論の対策方法2】スキマ時間に対策
SPIの勉強は60時間ほど必要と言われています。できるだけ多くの問題を解くことでSPIの問題に慣れていくため、スキマ時間を活用して対策するのも一つの手です。問題集を使った勉強は机などが必要ですが、近年はSPI対策のスマホアプリもリリースされているため、時間を有効活用できます。
キミスカが展開しているSPI対策アプリは、制限時間の機能がついているだけでなく、分野別の対策も可能です。移動中や空き時間に手軽にSPIの問題に触れられるため、忙しい就活生の心強い味方になってくれるでしょう。
【SPI推論の対策方法3】本番と同じ環境で受ける
SPIの推論対策をする際は、本番と同じ環境で模擬試験などを受けてみるのもおすすめです。本番と同じ制限時間で推論をはじめSPIの問題を解けるのかどうかを確認しましょう。ただし、SPIの検査時間は、Webテストやペーパーテストなどの形式によって異なる点に注意が必要です。
本番と同じ環境で対策する場合は、志望企業が実施するSPIの形式を調べておきましょう。以下の記事ではSPIの形式別に対策方法を紹介しています。自分が受検する検査の形式を確認したうえで、回答の時間配分を身につけましょう。
SPI推論の問題例
最後に、SPIの推論で実際に出される問題例を紹介します。ここで挑戦して解けないかもしれませんが、大切なのは何度もチャレンジして解き方を身につけることです。
一つ一つ丁寧に見ていきましょう。
【SPI推論の問題例】順序
【問題】
PQRSの4人チームで毎年恒例のサッカーの総当たり戦が行われた。
順位に関して次のことが分かっている。なお、同じ順位のチームはない。
Ⅰ Pは昨年より順位が3つ下だった。
Ⅱ Qは今年と昨年で順位が変わらなかった。
Ⅲ Rは今年2位であった。
今年の順位を左が上位として並べたとき、ただしいものを選べ。
<選択肢>
A. SRPQ
B. SRQP
C. PRSQ
D. RPQS
【解答・解説】
B. SRQP
Ⅰ、Ⅲより、次のことが分かる。昨年 P〇〇〇 今年 〇R〇P
これとⅡより、次のことが分かる。昨年 P〇Q〇 今年 〇RQP
よって、今年はSRQP
引用:【SPI 推論|非言語(数学)】練習問題から対策方法まで一挙公開!
【SPI推論の問題例】整数
【問題】
P、Q、Rはそれぞれボールを持っていて、次のことがわかっている。
Ⅰ 3人合わせて8個のボールを持っている。
Ⅱ PとQは同じ個数のボールを持っている。
Ⅲ RはPの2倍のボールを持っている。
このとき、Rは何個のボールを持っているか。
<選択肢>
A. 1
B. 2
C. 4
D. 5
E. 6
【解答・解説】
C. 4
Ⅱ、Ⅲの情報から、P=xとおくと、Q=x 、R=2xとなる。
さらにⅠの情報よりボールの個数の総和が8個だから、x + x +2x = 8 より、x=2であり、Rの持っている個数は4個。
引用:【SPI 推論|非言語(数学)】練習問題から対策方法まで一挙公開!
【SPI推論の問題例】割合
【問題】
あるラーメン屋の売上について調べたところ、前の月に対して20%ずつ増えている。この時、次の推論について述べたものとして、正しいものを選択肢の中で1つ選べ。
・このラーメン屋の売上は、この2ヶ月間で40%増加した
<選択肢>
A. 正しい
B. どちらともいえない
C. 誤り
【解答・解説】
C. 誤り
2ヶ月前を100とおくと、
1ヶ月後 100×1.2=120
2ヶ月後 120×1.2=144
と増加していくので、2ヶ月では最初より44%増加したことになる。
引用:【SPI 推論|非言語(数学)】練習問題から対策方法まで一挙公開!
【SPI推論の問題例】平均
【問題】
P、Q、R、Sの4人が100点満点のカラオケの採点をしたところ、次の結果になった。
Ⅰ 4人の平均点は60点だった。
Ⅱ QとRの平均点は50点であった。
Ⅲ SはPよりも10点高かった。
このとき、必ず正しいといえる推論の組み合わせはどれか。
<選択肢>
A. アだけ
B. イだけ
C. ウだけ
D. アとイ
E. アとウ
F. イとウ
G. アとイとウ
H. 正しい推論はない。
【解答・解説】
C. ウだけ
ア: SとQの点数の上下関係は分からないので、必ずしも正しいとは限らない。
イ: 少なくともQとRの点数の上下関係は分からないので、必ずしも正しいとは限らない。
ウ: 4人の合計点は60×4=240点。QとRの合計点は50×2=100点。よって、PとSの合計点は240-100=140点。よって、Sは、(140+10)÷2 = 75点。QとRの平均点は50点なので少なくともどちらかは75点以下である。よって、これは正しい。
引用:【SPI 推論|非言語(数学)】練習問題から対策方法まで一挙公開!
【SPI推論の問題例】位置
【問題】
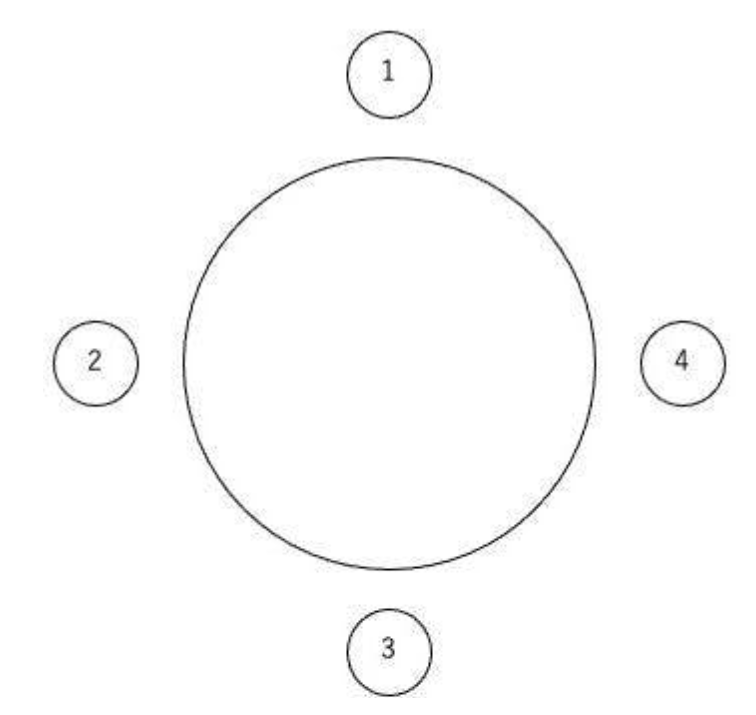
X 、Y、Zの3人が、円形に並んだ4つの席のいずれかに座っている。各自の座り方について、次のことが分かっている。
Ⅰ XとYは隣り合っていた。
Ⅱ 数字の2番の席は空席だった。
Zが座った可能性のある席の番号はいくつか。
<選択肢>
A. 1
B. 3
C. 4
D. 1か3
E. 1か4
F. 3か4
【解答・解説】
D. 1か3
2番が空席でXとYが隣り合っているので、XとYは(1、4)(4、3)の組み合わせで座っている。よって、Zは1か3。
引用:【SPI 推論|非言語(数学)】練習問題から対策方法まで一挙公開!
【SPI推論の問題例】正誤
【問題】X、Y、Zが同じ絵を見てて、次のように発言した。
X この絵には虎が描かれている。
Y この絵には少なくとも虎か龍が描かれている。
Z この絵には龍が描かれている。
全員が本当のことを言っているとは限らない。そこで、以下の推論がなされた。次のうち正しいものを一つ選びなさい。
<選択肢>
A. Yが正しければXは必ず正しい
B. Zが正しければYは必ず正しい
C. Xが正しければZは必ず正しい
【解答・解説】
B. Zが正しければYは必ず正しい
Yが正しいとしても、虎が入っていることは分からないため、Xは必ずしも正しくない。
Zが正しいとき、少なくとも龍は入っているため、Yは正しい。
Xが正しいとしても、龍が入っていることは分からないため、Zは必ずしも正しくない。
引用:【SPI 推論|非言語(数学)】練習問題から対策方法まで一挙公開!
【SPI推論の問題例】対戦(リーグ戦)
【問題】
X、Y、Z、Wの4人がテニスのリーグ戦をおこなった。勝敗について以下のことがわかっている。
Ⅰ YはXだけに負けた。
Ⅱ WはXに勝った
必ず正しいといえる推論はどれか。AからHで1つ選びなさい。ただし、引き分けはないものとする。
ア Xが1勝2敗なら、Wも1勝2敗
イ Zが全敗なら、Xは2勝1敗
ウ Wが1勝2敗なら、Xは2勝1敗
<選択肢>
A. アだけ
B. イだけ
C. ウだけ
D. アとイ
E. アとウ
F. イとウ
G. アとイとウ
H. 正しい推論はないYが正しければXは必ず正しい
【解答・解説】
B. イだけ
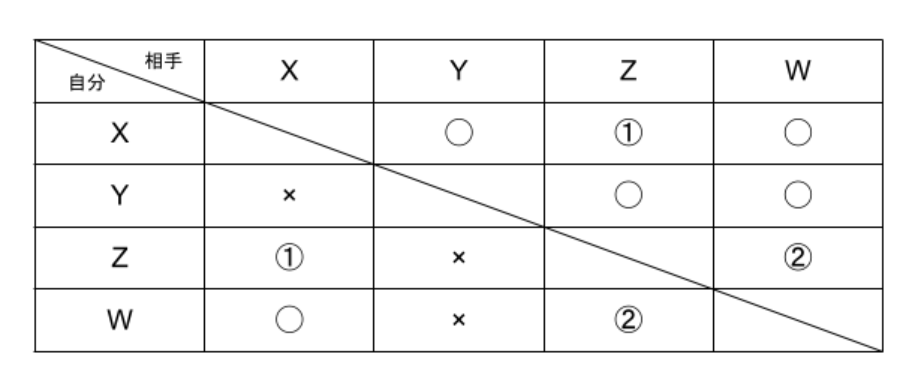
以上の図を参照する。
ア Xが1勝2敗なら、Wも1勝2敗 ←①が×で確定するが、②が確定しない
イ Zが全敗なら、Xは2勝1敗 ←①も②も×で確定する
ウ Wが1勝2敗なら、Xは2勝1敗 ←②が×で確定するが、①が確定しない
従ってイのみ正しい。
引用:【SPI 推論|非言語(数学)】練習問題から対策方法まで一挙公開!
【SPI推論の問題例】対戦(トーナメント戦)
【問題】
P、Q、R、S、T、U、V、Wの8チームがサッカーの大会でトーナメント戦を争った。対戦について次のⅠ〜Ⅲがわかった。
Ⅰ QはT、U、Wと戦った。ただし順不同である。
Ⅱ Pは2回戦で戦う可能性があったのはS、Uである。
Ⅲ Pが1回戦で戦ったのは、Rではない。
Pが1回戦で戦ったのはどのチームか。
<選択肢>
A. P
B. Q
C. R
D. S
E. T
F. U
G. V
H. W
【解答・解説】
G. V
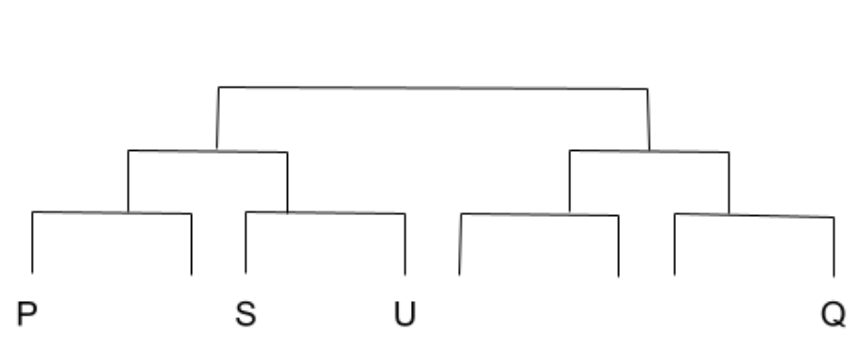
以上の図を参照する。
Ⅱより、SとUは1回戦で戦った。また、ⅠよりPとQは対戦していない。よって以上の図のようになる。QはT、U、Wと戦ったので、TとWは表の右半分にいる。また、Ⅲより答えはVとなる。
引用:【SPI 推論|非言語(数学)】練習問題から対策方法まで一挙公開!
SPI推論を解くコツは問題パターンを覚えること!
SPIの推論は、初見では難しく感じるかもしれません。しかし、SPIの問題は全体的にパターン化しているため、どういった問題が出るのかを事前に把握しておけば、素早く正解を選ぶことができます。そして、SPIの推論対策で重要なのは、問題を繰り返しとくことです。何度も解いているうちに問題のパターンや解き方を覚えられます。ぜひ本記事で紹介したポイントを参考に、SPIの推論を攻略してみましょう。

